قانون اهرم،Tie Lines and the Lever Rule

Tie Lines and the Lever Rule    
          

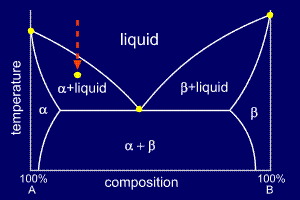
Consider a cooling alloy at the composition and temperature marked on the diagram. As shown on the phase diagram, the alloy is, at the given temperature, a mixture of alpha and liquid phases - but what are their exact compositions at this temperature?

        

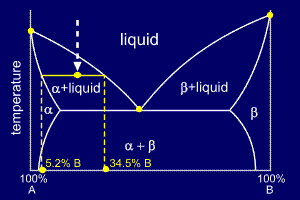
An isothermal (constant temperature) line through the alloy's position on the phase diagram when it is in a two phase field, intersecting the two adjacent solubility curves, is called a tie line (yes, that's the horizontal yellow line on the diagram).
The ends of the tie lines show the compositions of the two phases that exist in equilibrium with each other at this temperature. From the diagram we know that alpha and liquid phases will exist. The tie line shows that the alpha phase is 5.2%B and the liquid phase is 34.5%B at this temperature.
Remember, though, that the overall composition of the sample is unchanged - we are only discovering the compositions of the constituent phases within the sample.
  
        

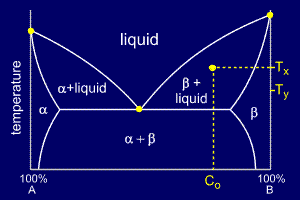
For a cooling alloy at composition Co and temperature Tx , tie lines may be used to answer questions such as:
•what phases are present ?
•what are their compositions ?
•if the temperature is reduced to Ty, how do the compositions of the two phases vary ?
The answer to "what phases are present ?" is easy. Composition Co and temperature Tx meet in the beta + liquid phase field, so these are the two phases present.

 

To answer "what are their compositions ?" we must draw a horizontal tie line from the point to the nearest phase diagram boundaries. The tie line shows us that the compositions are:
•Liquid: X wt% B
•Beta: Y wt% B
Tie Lines and the Lever Rule    
        

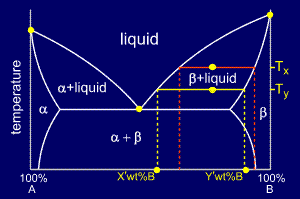
To answer the last question "if the temperature is reduced to Ty, how do the compositions of the two phases vary?" consider the new tie-line, shown in yellow on the diagram.
The compositions of liquid and beta phase have both decreased in wt%B to:
•Liquid: X' wt% B
•Beta: Y' wt% B
Thus, both the liquid and the beta phases are getting richer in A as the sample is cooled.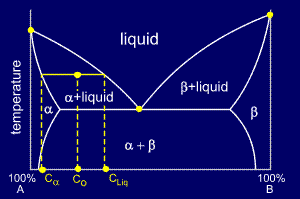
 
 
Now that we know the compositions of the two phases, we need to find how much of each phase exists at the given temperature. The ratio of the two phases present can be found by using the lever rule.
At first sight the lever rule can appear confusing. It is really invoking the conservation of mass, and can be proved mathematically, as shown below the diagram.

Essentially, we start off with an overall composition of our alloy - Co. From the tie-line we know that the two phases at a given temperature have two different compositions, but overall the amounts of these two compositions must add up to the alloy's overall composition, Co.
This is the basis for the lever rule. Using the lever rule itself is very simple, we'll show you with a diagram.....
 

 
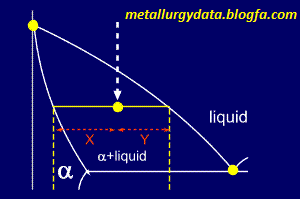
Basically, the proportions of the phases present are given by the relative lengths of the tie line. So, the proportions of alpha and liquid present on the diagram (showing a portion of the whole phase diagram) are:
 and  
Simple, isn't it ?
But... which equation corresponds to which phase ?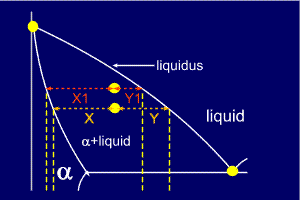

Now, consider the same alloy as it crosses the liquidus line. It seems reasonable to assume that, at this point, the alloy will be nearly all liquid. Looking at the diagram it can be seen that Y1 is very small here and so must be the proportion of alpha present. Similarly X1 is relatively large and so it corresponds to the amount of liquid.
So, the left side of the tie line gives the proportion of the liquid phase (the phase to the right), and the right side of the tie line gives the proportion of the alpha phase (the phase on the left).
Remember: you use the length of the line which is furthest from the phase in which you are interested.

  
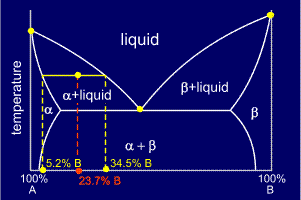
Distances along the tie line can be found very simply by using a ruler on an accurate phase diagram or, more correctly, by using data from the composition axis (the x-axis).
For example, on the diagram shown, the percentage of alpha present can be calculated from the three pieces of composition data given:
Fraction of alpha = (34.5 - 23.7) / (34.5 - 5.2) = 0.3686
Thus, percentage of alpha = 0.3686 x 100 = 36.86%
and, as the alpha and the liquid make up 100% of the alloy's composition:
Percentage of liquid = 100 - 36.86 = 63.14%